Los matemáticos Urtzi Buijs y Miriam González demuestran cómo se pueden sumar números cuadrados con sencillas figuras
FUENTE: ABC
En un artículo reciente del «ABCdario de las matemáticas» hablábamos de «La sociedad secreta de Pitágoras y el «superpoder» de los números figurados». Explicábamos cómo obtener el resultado de algunas sumas complejas solo observando un dibujo, sin necesidad de coger el boli y hacer sesudas operaciones. También contábamos la anécdota (probablemente apócrifa) de un jovencísimo Gauss sorprendiendo a su maestro de aritmética sumando 1+2+3+…+100=5050. Este resultado puede calcularse con la fórmula 1+2+…+n= n(n+1)/2 para el valor n=50, pero también se deduce de un solo vistazo a la figura adjunta:
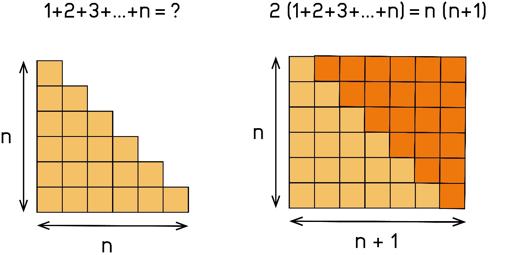
Pero en el artículo citado dejábamos en el tintero una pregunta, ¿puede alguna mente privilegiada realizar una hazaña mayor y con un argumento visual sumar los primeros números cuadrados: 1^2+2^2+3^2+….+n^2 ? ¡Vamos convencer al lector de que esto puede hacerse! Y además sin apenas pestañear.
Consideremos para este problema pequeños cubitos como unidad. Queremos sumar los siguientes cubitos:
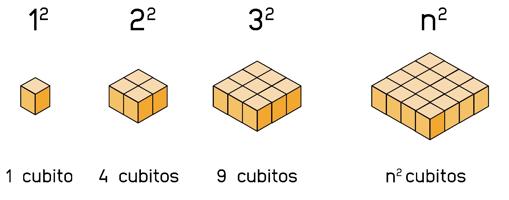
Lo cual equivale a contar cuántos cubitos hay en la siguiente pirámide,
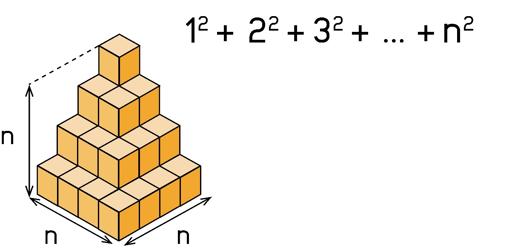
Que vista desde atrás tiene esta pinta, ¿verdad?
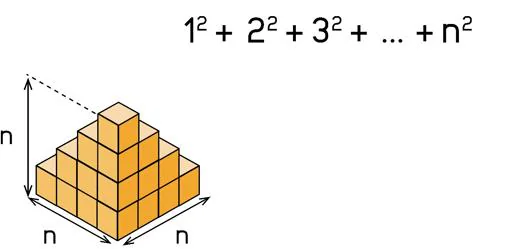
Vamos a hacer algo similar a lo que hicimos para sumar 1+2+3+…+n cuando duplicamos el triángulo formado por los cuadraditos para formar un rectángulo.
En este caso consideramos TRES pirámides con 1^2+2^2+3^2+…+n^2 cubitos cada una.
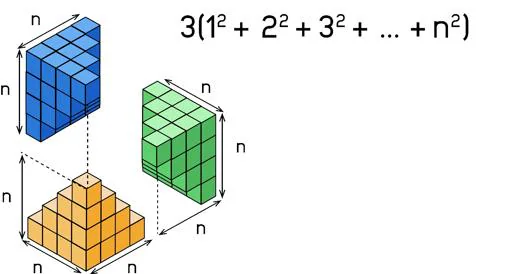
Estas tres pirámides podemos acoplarlas como se indica en la figura, pero a diferencia del caso anterior en el que los dos triángulos de cuadraditos acoplados formaban un rectángulo, en este las tres pirámides de cubitos acoplados no forman un ladrillo perfecto (figura que recibe el nombre de ortoedro). Lo que obtenemos es un bloque de ancho n, largo n+1 y en dos alturas (¡hay un escalón en la azotea!).
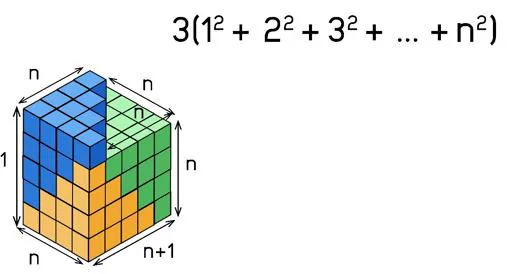
Pero, si nos fijamos, los dos niveles que hay en la azotea son congruentes, de modo que podríamos recortar el nivel de mayor altura por la mitad y rellenar el nivel de menor altura, aplanando la azotea sin que hayamos quitado ni añadido cubo alguno al edificio.
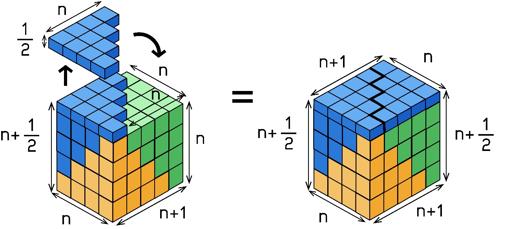
Ahora podemos contar el número de cubitos de este bloque sin más que multiplicar, largo x ancho x alto. Tenemos entonces que
3 (1^2+2^2+3^2+…+n^2) = n(n+1)(n+ ½ )
La única pequeña cuenta que tenemos que hacer es sumar n con ½
3 (1^2+2^2+3^2+…+n^2) = n(n+1)((2n+1)/2)
Y despejar la expresión buscada
1^2+2^2+3^2+…+n^2 = n(n+1)(2n+1)/6.
¡No está nada mal!
¡¡El siguiente paso sería atreverse con la suma de los primeros n cubos 1^3+2^3+3^3+-…+n^3 !!
Curiosamente, esta suma tiene una expresión realmente simple y sorprendente.
1^3+2^3+3^3+…+n^3 = (1+2+3+…+100)^2
Este resultado recibe el nombre de Teorema de Nicómaco en honor a Nicómaco de Gerasa, matemático y filósofo que vivió en Siria entre los años 60 y 120 d.C.
Nicómaco, considerado neopitagórico, es conocido por su Manual de Armónicos y su Introducción a la Aritmética.
Para probar tan elegante teorema vamos a comenzar por representar el miembro izquierdo de la ecuación 1^3+2^3+3^3+…+n^3 = (1+2+3+…+100)^2 como suma de bloques formados por cubitos:
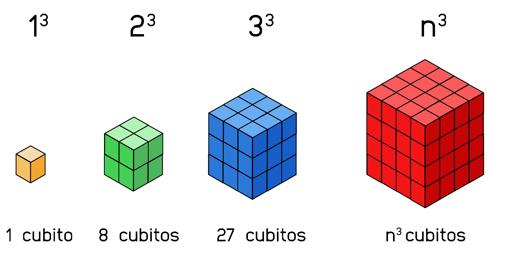
Hagamos lo siguiente, cada uno de estos bloques cúbicos los separaremos por pisos. En los bloques de lado par separaremos además el último piso por la mitad.
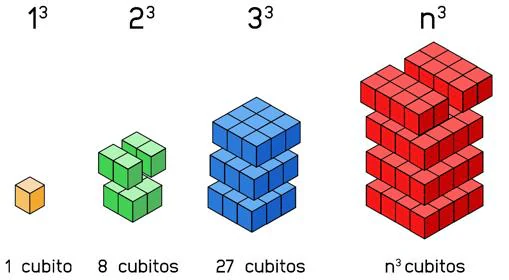
Con cada uno de estos cubos descompuestos en piezas podemos construir una figura formando un ángulo recto.
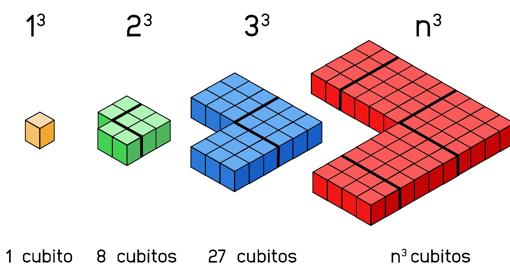
Y estos ángulos encajan perfectamente cada uno con el siguiente formando un cuadrado perfecto.
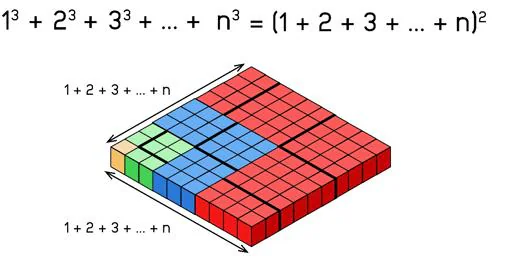
¿Cuántos cuadraditos tenemos en este tapiz multicolor? Por una parte sabemos que hay 1^3+2^3+3^3+….+n^3 . Pero por otra parte podemos contarlos simplemente multiplicando lado por lado de este cuadrado, y dado que el lado tiene 1+2+3+…+n cuadrados, obtenemos que hay un total de (1+2+3+…+100)^2 .
¡Hemos probado el teorema de Nicómaco visualmente!
Pero en vez de tener que idear una demostración ingeniosa para cada caso particular, ¿No existirá una fórmula para el caso general 1^p+2^p+3^p+….+n^p, para cualquier número natural p?
La respuesta es afirmativa, pero eso ya es otra historia del ABCdario de las matemáticas en la que conoceremos a nuevos personajes, el matemático suizo Jakob Bernoulli, el matemático japonés Seki Kōwa, y a la matemática británica Ada Lovelace, ¡pionera de la programación informática!















