La nueva entrega del ABCdario de las Matemáticas muestra cómo en muestras de números de datos arbitrarios unos números aparecen más que otros
FUENTE: ABC
Si tomamos una fuente de datos basada en números que aparecen en la vida cotidiana, como pueden ser, el importe de las facturas de la luz, los números de las calles de una ciudad o los valores de las acciones en bolsa, parece lógico pensar que los dígitos del 1 al 9 aparecen en estas cifras de forma totalmente aleatoria.
Por esto, si nos fijamos en el primer dígito de todos estos datos cabe esperar que las cifras del 1 al 9 aparezcan en la primera posición un número similar de veces, es decir el 1 aparece en primer lugar aproximadamente el 11,1% de las veces, el 2 aparece en primer lugar el 11,1% de la veces y así sucesivamente.
Nada más lejos de la realidad, ya que las muestras tomadas del mundo real parece que sienten cierta predilección por poner en primer lugar algunos dígitos en concreto.
Corría el año 1881 cuando el astrónomo y matemático Simon Newcomb publicó su artículo «Note on the frequency of use of the diferent digits in natural numbers» en el número 4 del «American Journal of Mathematics». Según se cree, observando libros de logaritmos –herramienta muy usada por los astrónomos de la época- se dio cuenta de que las primeras páginas de dichos libros estaban más desgastadas. Éstas páginas eran aquellas en las que aparecían los números que empezaban por 1.
Este hecho observado por Newcomb fue el que le llevó a formular el siguiente principio:
«En una lista de números tomada de un conjunto arbitrario de datos hay más números que comienzan por 1 que con cualquier otro dígito»
Algunos años más tarde el físico Frank Benford publicó el artículo «The law of anomalous numbers» en el número de abril de 1938 de los «Proceedings of the American Philosophical Society». En dicho trabajo enuncia la que ha venido a ser llamada ley Benford, o ley del primer dígito y que describe la frecuencia con la que aparecen, en primer lugar, los dígitos del 1 al 9, en datos de la vida cotidiana. Benford determinó que esta frecuencia viene dada por la función:
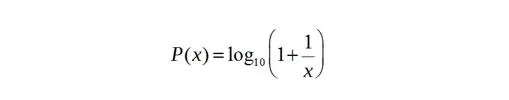
donde es x el valor de la cifra en cuestión y P (x) es la probabilidad de que dicha cifra aparezca en primer lugar. Gráficamente esta función se puede representar como sigue:
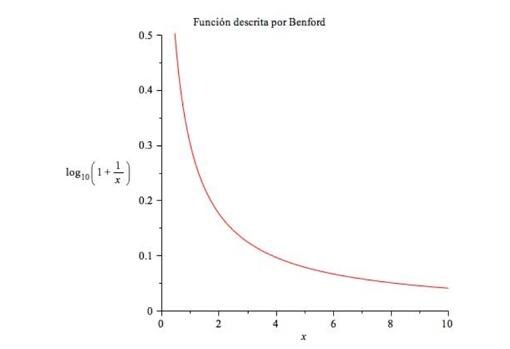
Por lo tanto, según la función dada por Benford la frecuencia de aparición de las cifras del 1 al 9 como primer dígito (en una serie de datos tomados de la vida real) es la siguiente:

Así, si tomamos una lista grande de datos, estas cifras empezarán por 1 el 30,1% de las veces, por 2 un 17,6% de las veces y así sucesivamente.
Desde un punto de vista teórico todo esto esta muy bien, pero si tomamos datos reales ¿será cierto que se ajustan a la curva descrita por Benford?
Para comprobar que este fenómeno es real (y no sólo teórico) me he tomado la libertad de mirar los datos del censo de 2019 del Instituto Nacional de Estadística (INE). Estos datos son públicos y se pueden buscar como «Cifras de población resultantes de la Revisión del Padrón Municipal a 1 de enero de 2019. Datos por municipios». Observando los datos de las poblaciones de los 8131 municipios españoles, (lo cual, dicho sea de paso, lleva un rato pero) se tiene que la aparición de las cifras del 1 al 9 como primer dígito es la siguiente:

Podemos representar gráficamente estos datos como sigue:
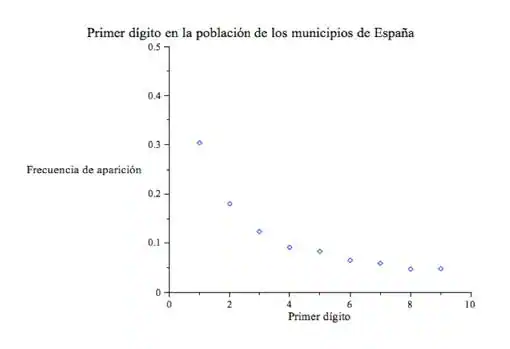
A primera vista, parece que los datos reales y los predichos por Benford se parecen mucho, basta comparar la última fila de las tablas 1 y 2. Pero puesto que una imagen vale más que mil palabras, en la siguiente figura se presentan en una misma gráfica ambos datos (los reales y los predichos por la Ley Benford).

Según parece los datos reales se ajustan muy, muy bien al comportamiento esperable según la ley Benford.
Desde un punto de vista más actual, en el año 2012 Mark Nigrini publicó su trabajo «Benford’s Law: Applications for forensic Accounting, Auditing and Fraud Detection» donde mostraba cómo este comportamiento de los números obtenidos del mundo real permite identificar si un conjunto de datos proviene de una fuente real o si por el contrario se trata de datos falsos. Puesto que «poderoso caballero es don dinero» una de las mayores aplicaciones que se ha encontrado a la ley Benford es que es capaz de determinar, entre otras cosas, la veracidad o falsedad de las facturas presentadas en las declaraciones de la renta.










